平衡二叉搜索树（AVL）

c++ • 489 • 0

tgw 8 月前

二叉搜索树又称AVL，他比之二叉搜索树（前面文件介绍了）多了一个重要的特性，左右子树高度差不能超过一，而这个特性是由平衡因子决定的，今天主播就带领大家手搓一个平衡二叉搜索树。

首先是节点的创建，我们依旧依照以前的二叉搜索树写，只不过多了parent指针和平衡因子。代码如下： template
struct AVLTreeNode
{
pair _kv;
AVLTreeNode* _left;
AVLTreeNode* _right;
AVLTreeNode* _parent;

int _bf; // balance factor

AVLTreeNode(const pair& kv)
    :_kv(kv)
    , _left(nullptr)
    , _right(nullptr)
    , _parent(nullptr)
    , _bf(0)
{
}

};

后面就是增加操作也是难点之一：单纯插入只需要按照平衡搜索树的操作进行正常key比较插入即可，但是如果是平衡搜索二叉树，我们就必须考虑平衡因子的破坏，以及调整。当我们计算平衡因子时需要计算几种情况，插入节点的父节点平衡因子确定。当从左插入时就需要parent->bf就需要减一，当从右边插入时平衡因子就需要加一。在平衡因子变化循环加减一轮后我们需要判断三种情况： 1.parent->bf==0 说明没有变化之前是-1或1，此时就不需要继续循环，不影响上面父节点的平衡因子。 2.parent->bf==1或-1，说明原来平衡因子为0，此时就需要继续循环。 3.parent->bf==-2或者2,此时我们不仅需要继续循环，还需要对二叉树进行旋转，因为此时二叉树的平衡性已经完全被破坏了。

旋转有四种情况： 1.左单旋 2.右单旋 3.左右单旋 4.右左单旋

如图所示：

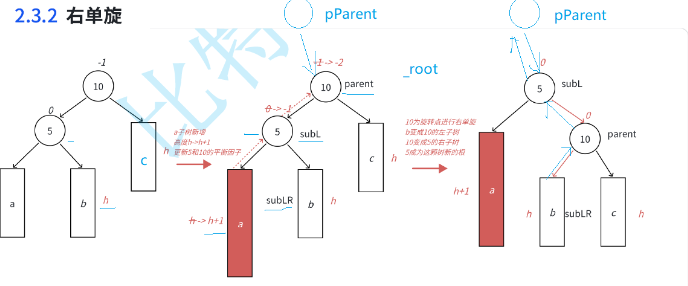
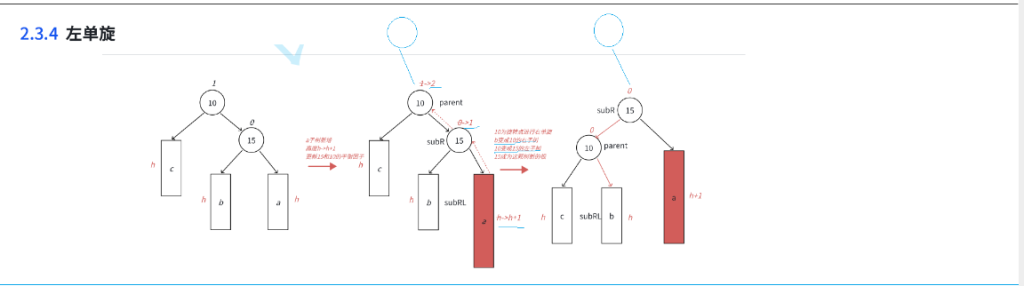
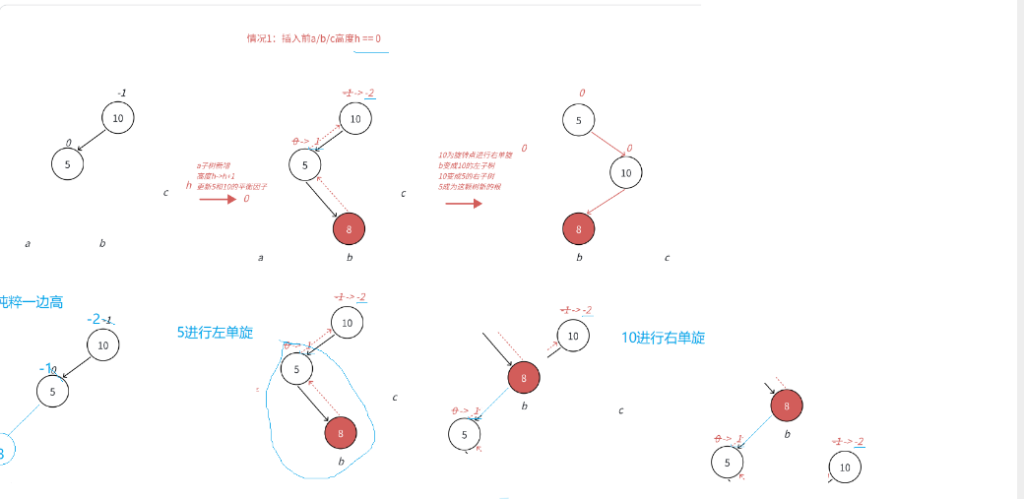
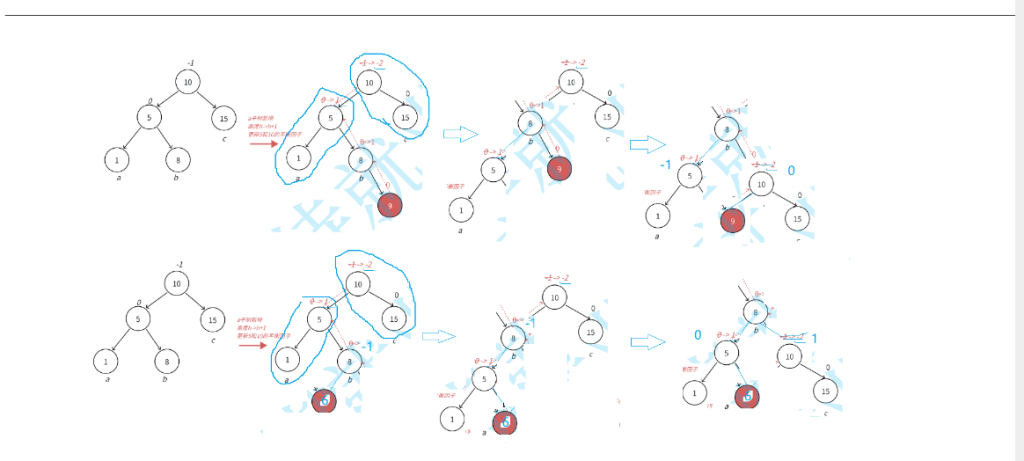
单旋转时平衡因子的调整都是有规律可循，但是双旋转时，平衡因子的调整就比较复杂，大致分三种情况：举例说明：

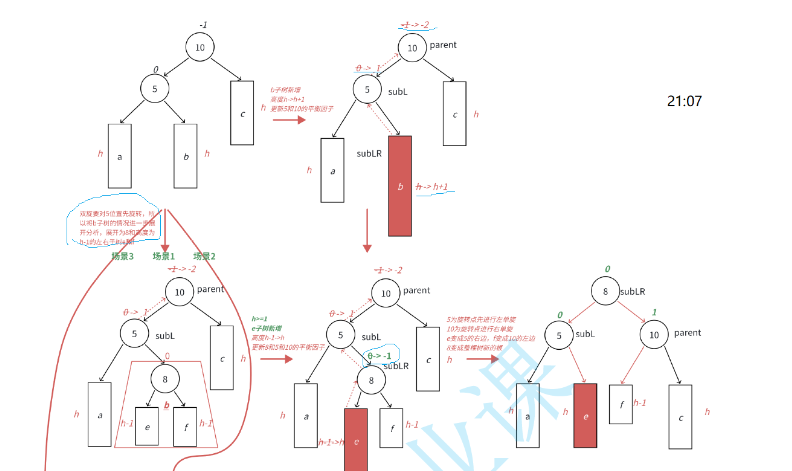
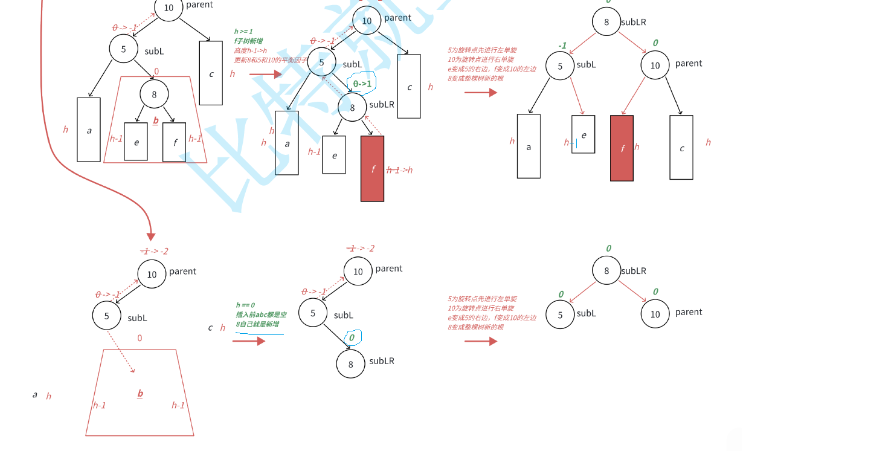
下面是代码实现：

bool Insert(const pair& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}

Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
    if (cur->_kv.first < kv.first)
    {
        parent = cur;
        cur = cur->_right;
    }
    else if (cur->_kv.first > kv.first)
    {
        parent = cur;
        cur = cur->_left;
    }
    else
    {
        return false;
    }
}

cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
    parent->_right = cur;
}
else
{
    parent->_left = cur;
}
// 链接父亲
cur->_parent = parent;

// 控制平衡
// 更新平衡因子
while (parent)
{
    if (cur == parent->_left)
        parent->_bf--;
    else
        parent->_bf++;

    if (parent->_bf == 0)
    {
        break;
    }
    else if (parent->_bf == 1 || parent->_bf == -1)
    {
        cur = parent;
        parent = parent->_parent;
    }
    else if (parent->_bf == 2 || parent->_bf == -2)
    {
        if (parent->_bf == -2 && cur->_bf == -1)
        {
            RotateR(parent);
        }
        else if (parent->_bf == 2 && cur->_bf == 1)
        {
            RotateL(parent);
        }
        else if (parent->_bf == -2 && cur->_bf == 1)
        {
            RotateLR(parent);
        }
        else if (parent->_bf == 2 && cur->_bf == -1)
        {
            RotateRL(parent);
        }
        else
        {
            assert(false);
        }

        break;
    }
    else
    {
        assert(false);
    }
}


return true;

}

void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;

parent->_left = subLR;
if (subLR)
    subLR->_parent = parent;

Node* pParent = parent->_parent;

subL->_right = parent;
parent->_parent = subL;

if (parent == _root)
{
    _root = subL;
    subL->_parent = nullptr;
}
else
{
    if (pParent->_left == parent)
    {
        pParent->_left = subL;
    }
    else
    {
        pParent->_right = subL;
    }

    subL->_parent = pParent;
}

subL->_bf = 0;
parent->_bf = 0;

}

void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;

Node* parentParent = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (parentParent == nullptr)
{
    _root = subR;
    subR->_parent = nullptr;
}
else
{
    if (parent == parentParent->_left)
    {
        parentParent->_left = subR;
    }
    else
    {
        parentParent->_right = subR;
    }
    subR->_parent = parentParent;
}

parent->_bf = subR->_bf = 0;

}

void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;

RotateL(parent->_left);
RotateR(parent);

if (bf == -1)
{
    subLR->_bf = 0;
    subL->_bf = 0;
    parent->_bf = 1;
}
else if (bf == 1)
{
    subLR->_bf = 0;
    subL->_bf = -1;
    parent->_bf = 0;
}
else if (bf == 0)
{
    subLR->_bf = 0;
    subL->_bf = 0;
    parent->_bf = 0;
}
else
{
    assert(false);
}

}

void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 0)
{
subR->_bf = 0;
subRL->_bf = 0;
parent->_bf = 0;
}
else if (bf == 1)
{
subR->_bf = 0;
subRL->_bf = 0;
parent->_bf = -1;
}
else if (bf == -1)
{
subR->_bf = 1;
subRL->_bf = 0;
parent->_bf = 0;
}
else
{
assert(false);
}
}

接下来就是查找，与前面大差不差：

Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < key) { cur = cur->_right;
}
else if (cur->_kv.first > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}

return nullptr;

}

遍历，高度，数量，平衡性检查：

void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}

_InOrder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_InOrder(root->_right);

}

int _Height(Node* root)
{
if (root == nullptr)
return 0;
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

int _Size(Node* root)
{
if (root == nullptr)
return 0;

return _Size(root->_left) + _Size(root->_right) + 1;

}

bool _IsBalanceTree(Node* root)
{
// 空树也是AVL树
if (nullptr == root)
return true;
// 计算pRoot结点的平衡因子：即pRoot左右子树的高度差
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
int diff = rightHeight – leftHeight;

// 如果计算出的平衡因子与pRoot的平衡因子不相等，或者
// pRoot平衡因子的绝对值超过1，则一定不是AVL树
if (abs(diff) >= 2)
{
    cout << root->_kv.first << "高度差异常" << endl;
    return false;
}

if (root->_bf != diff)
{
    cout << root->_kv.first << "平衡因子异常" << endl;
    return false;
}

// pRoot的左和右如果都是AVL树，则该树一定是AVL树
return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);

}

最后就是删除了，删除借鉴插入还是很容易写出来的

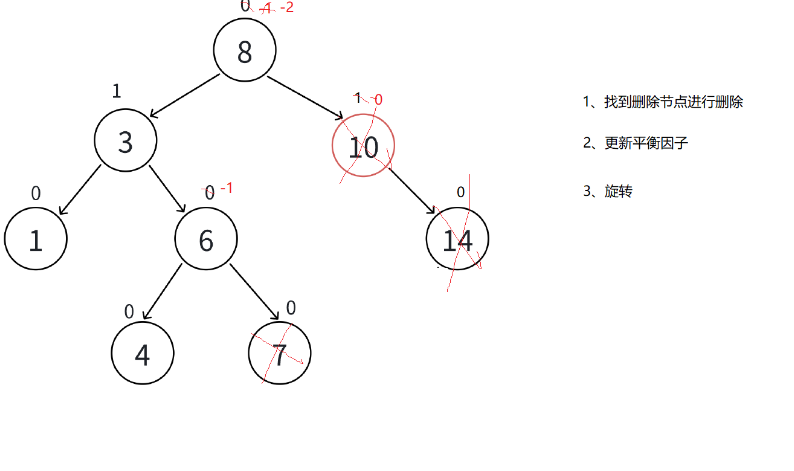
代码实现：bool _eraser(const K& key) {
Node* node = Find(key);
Node* parent = node->_parent;
if (node == nullptr) return false; // 如果节点不存在，返回false
else {
if (node->_left == nullptr) { // 左孩子为空
if (node == _root) { // 如果是根节点
_root = node->_right;
}
else {
if (node->_parent->_left == node) { // 如果是左孩子
node->_parent->_left = node->_right;
if (node->_right) node->_right->_parent = node->_parent;
node->_parent->_bf++;
}
else { // 如果是右孩子
node->_parent->_right = node->_right;
if (node->_right) node->_right->_parent = node->_parent;
node->_parent->_bf–;
}
}
delete node;
}
else if (node->_right == nullptr) { // 右孩子为空
if (node == _root) { // 如果是根节点
_root = node->_left;
}
else {
if (node->_parent->_left == node) { // 如果是左孩子
node->_parent->_left = node->_left;
if (node->_left) node->_left->_parent = node->_parent;
node->_parent->_bf++;
}
else { // 如果是右孩子
node->_parent->_right = node->_left;
if (node->_left) node->_left->_parent = node->_parent;
node->_parent->_bf–;
}
}
delete node;
}
else { // 左右孩子都不为空
Node* replaceparent = node;
Node* replace = node->_right; // 替代节点，左子树最左节点
while (replace->_left) {
replaceparent = replace;
replace = replace->_left;
}
node->_kv.first = replace->_kv.first;
if (replaceparent->_left == replace) {
replaceparent->_left = replace->_right;
if (replace->_right) replace->_right->_parent = replaceparent;
}
else {
replaceparent->_right = replace->_right;
if (replace->_right) replace->_right->_parent = replaceparent;
}
parent = replace->_parent;
delete replace;
}
// 更新平衡因子并调整平衡
Node* cur = parent;
while (cur) {
if (cur->_bf == 2 || cur->_bf == -2) {
if (cur->_bf == -2 && cur->_left->_bf == -1) {
RotateR(cur);
}
else if (cur->_bf == 2 && cur->_right->_bf == 1) {
RotateL(cur);
}
else if (cur->_bf == -2 && cur->_left->_bf == 1) {
RotateLR(cur);
}
else if (cur->_bf == 2 && cur->_right->_bf == -1) {
RotateRL(cur);
}
else {
assert(false);
}
break;
}
cur = cur->_parent;
}
}
return true;
}

如有错误欢迎指出，今天的更新就到这里了！

12 赏

‹ 上一篇

下一篇 ›

作者尚未添加打赏二维码！

平衡二叉搜索树（AVL）

相关文章

评论

我是萌萌哒的侧边栏！