快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
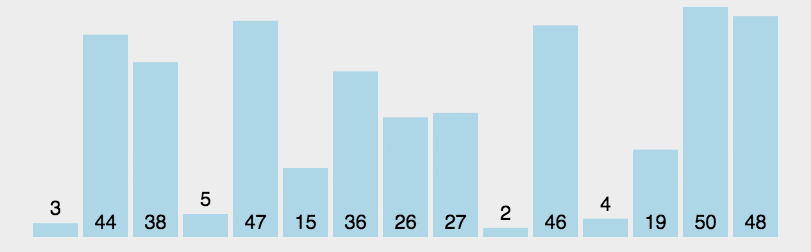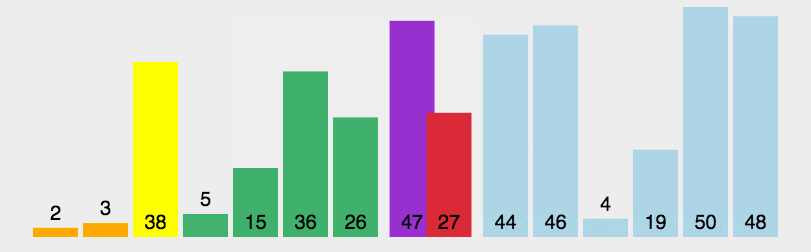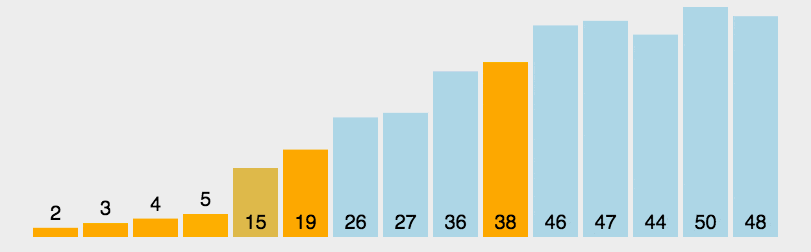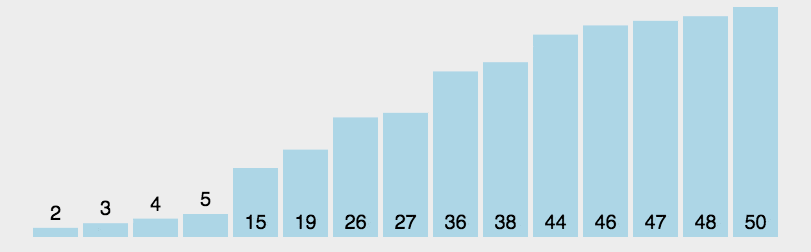
上图为快速排序演示图:
其核心思想是从两端向中间扫描,高效地将数组分为两部分。
实现步骤
- 选基准值
通常选第一个元素作为基准(pivot = arr[low])。 - 双指针扫描
- 左指针
i:从low开始向右找大于等于pivot的元素。 - 右指针
j:从high开始向左找小于等于pivot的元素。 - 交换
arr[i]和arr[j],直到i和j相遇。
- 左指针
- 终止条件
当i >= j时停止,此时j的位置即为分区点(pivot应插入的位置)。 - 递归排序
对low到j和j+1到high的子数组递归排序。
下面是代码演示:
void quicksort(vector& t, int left, int right) {
int key = t[left];
int end = right, begin = left + 1;
while (begin < end) {
while (beginkey) {
begin++;
}
while (begin优化 1.看了上述代码思路,我们会出现一个想法,如果将其均匀二分可能很像一颗二叉树,而二叉树的叶子节点占全数的一半,此时我们是否可以优化快排呢?所以我们可以这样操作,在遍历最后几个区间时进行小区间优化,使用插入排序去排序接下来的部分
2.还有一个问题要是每次都是在数组最后或最前相遇岂不是时间复杂度变成了O(n^2),于是我们需要随机选择一个key值,博主这里的实现思路是选择left,right,(left+right)/2,里面中间的那个数去解决。

下面是优化后的代码:
int GetMidi(int* a, int left, int right)
{
int midi = (left + right) / 2;
// left midi right
if (a[left] < a[midi])
{
if (a[midi] < a[right])
{
return midi;
}
else if (a[left] < a[right])
{
return right;
}
else
{
return left;
}
}
else // a[left] > a[midi]
{
if (a[midi] > a[right])
{
return midi;
}
else if (a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}
// 避免有序情况下,效率退化
// 1、随机选key
// 2、三数取中
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
// 小区间优化,不再递归分割排序,减少递归的次数
if ((right - left + 1) < 10)
{
InsertSort(a+left, right - left + 1);
}
else
{
// 三数取中
int midi = GetMidi(a, left, right);
Swap(&a[left], &a[midi]);
int keyi = left;
int begin = left, end = right;
while (begin < end)
{
// 右边找小
while (begin < end && a[end] >= a[keyi])
{
--end;
}
// 左边找大
while (begin < end && a[begin] <= a[keyi])
{
++begin;
}
Swap(&a[begin], &a[end]);
}
Swap(&a[keyi], &a[begin]);
keyi = begin;
// [left, keyi-1] keyi [keyi+1, right]
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
}今天的更新就到这里,如有错误,欢迎指出,谢谢
评论
还没有任何评论,你来说两句吧!