代码仓库:https://gitee.com/tgwTTT/data-structure/tree/master/Gragh
并查集原理
在一些应用问题中,需要将n个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个单元素集合,然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find set)。
比如当在10个人内,我认识你,你认识他,我们三个就叫做一个小团体,若要求有几个小团体呢?
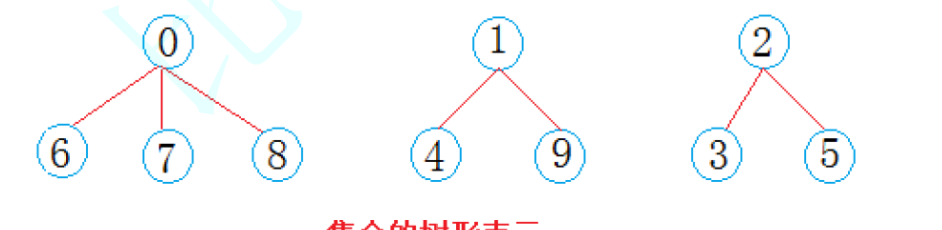
此时我们并查集就发挥作用了。
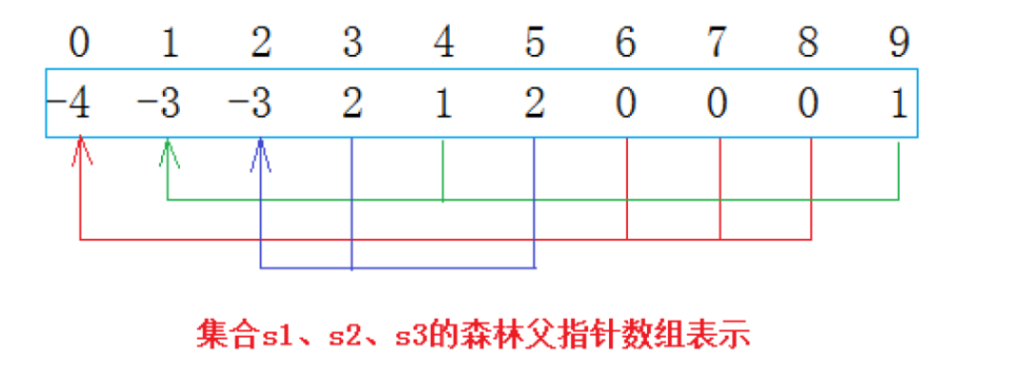
数组下标表示父节点下标,若为负则表示其为父节点
先将全体数据置为-1,如若两者间有关系,则找到两人的父节点选择其中一个作为另一个父节点,将其值置为其父节点的下标。
最后寻找其中有几个负数,判断其有几个小团体
下面是代码实现
class UnionFindSet
{
public:
UnionFindSet(size_t n):_ufs(n,-1) {}
void Union(int x1, int x2) {//合并
int root1 = FindRoot(x1);
int root2 = FindRoot(x2);
if (root1 == root2) {
return;
}
else {
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}
}
int FindRoot(int x) {
int parent = x;
while (_ufs[parent]>=0) {
parent = _ufs[parent];
}
return parent;
}//找根
bool Inset(int x1,int x2){
return FindRoot(x1) == FindRoot(x2);
}//是否在同一个集合
size_t SetSize(){
int count = 0;
for (auto i : _ufs) {
if (i < 0)count++;
}
return count;
}//有几个集合
private:
vector_ufs;
};
但是出现了一个新问题,即每当树的深度非常大时,就会影响到我们的效率
下面是解决方法:
每次寻找根节点时,每当深度超过2时,都将其挂在根节点下:
int FindRoot(int x) {
int parent = x;
while (_ufs[parent]>=0) {
parent = _ufs[parent];
}
_ufs[x] = parent;//路径压缩
return parent;
}//找根下面是题目练习:
答案:
class Solution {
public:
int findCircleNum(vector>& isConnected) {
// 手动控制并查集
vector ufs(isConnected.size(), -1);
// 查找根
auto findRoot = [&ufs](int x) {
while (ufs[x] >= 0)
x = ufs[x];
return x;
};
for (size_t i = 0; i < isConnected.size(); ++i) {
for (size_t j = 0; j < isConnected[i].size(); ++j) {
if (isConnected[i][j] == 1) {
// 合并集合
int root1 = findRoot(i);
int root2 = findRoot(j);
if (root1 != root2) {
ufs[root1] += ufs[root2];
ufs[root2] = root1;
}
}
}
}
int n = 0;
for (auto e : ufs) {
if (e < 0)
++n;
}
return n;
}
};
今天的跟新就到这,如有不对欢迎评论区指出!!
评论
还没有任何评论,你来说两句吧!