完整代码:https://gitee.com/tgwTTT/data-structure/tree/master/Btree
B树(B-Tree)是一种多路平衡查找树,广泛应用于数据库和文件系统。相比二叉搜索树,B树每个节点可以存储多个关键字和子节点,极大地降低了树的高度,提高了查找和插入效率,尤其适合磁盘存储场景。
一、B树的结构
以如下代码为例,定义了一个阶数为 M 的 B树节点:
template
struct BTreeNode
{
K _keys[M]; // 存储关键字
BTreeNode* _subs[M+1]; // 存储子节点指针
BTreeNode* _parent; // 父节点指针
size_t _n; // 当前关键字数量
// 构造函数略
}; 每个节点最多存储 M 个关键字和 M+1 个子节点。节点的关键字有序排列,子节点指向关键字区间
结构图示(以 M=3 为例)
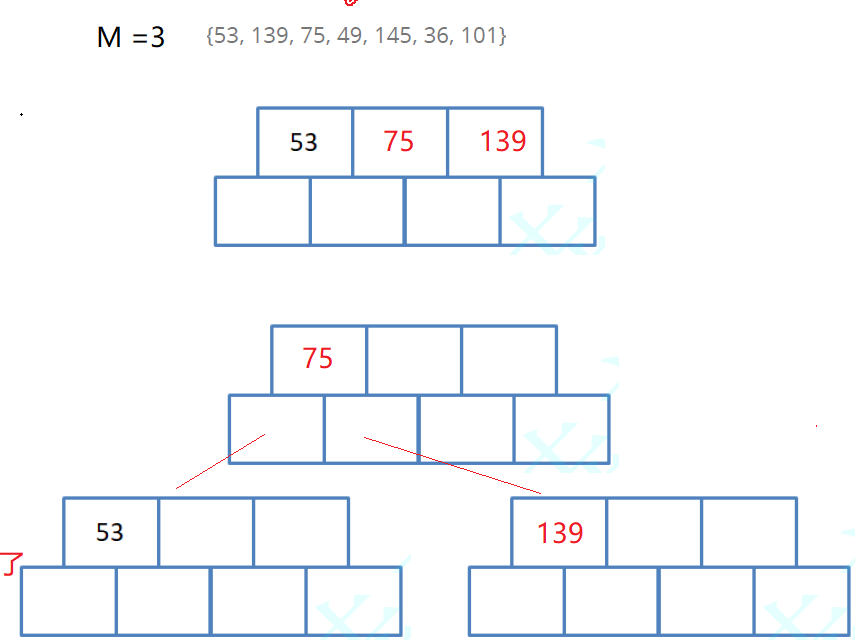
二、B树的插入与分裂操作
1. 插入流程
插入时,首先查找合适的叶子节点,然后插入关键字。如果节点未满,直接插入;如果节点已满,则需要分裂。
void InsertKey(Node* node, const K& key, Node* child)
{
int end = node->_n - 1;
while (end >= 0 && key < node->_keys[end])
{
node->_keys[end + 1] = node->_keys[end];
node->_subs[end + 2] = node->_subs[end + 1];
--end;
}
node->_keys[end + 1] = key;
node->_subs[end + 2] = child;
if (child) child->_parent = node;
node->_n++;
}2. 节点分裂
当插入后节点关键字数达到 M,需要分裂节点:
- 取中间关键字(midKey),将其提升到父节点。
- 将右半部分关键字和子节点分裂到新节点(brother)。
- 如果父节点也满了,继续向上分裂,直到根节点。
代码片段(分裂过程)
size_t mid = M / 2;
Node* brother = new Node;
size_t j = 0;
size_t i = mid + 1;
for (; i <= M - 1; ++i)
{
brother->_keys[j] = parent->_keys[i];
brother->_subs[j] = parent->_subs[i];
if (parent->_subs[i]) parent->_subs[i]->_parent = brother;
++j;
parent->_keys[i] = K();
parent->_subs[i] = nullptr;
}
brother->_subs[j] = parent->_subs[i];
if (parent->_subs[i]) parent->_subs[i]->_parent = brother;
parent->_subs[i] = nullptr;
brother->_n = j;
parent->_n -= (brother->_n + 1);
K midKey = parent->_keys[mid];
parent->_keys[mid] = K();3. 分裂图示
假设 M=3,插入后节点满了:
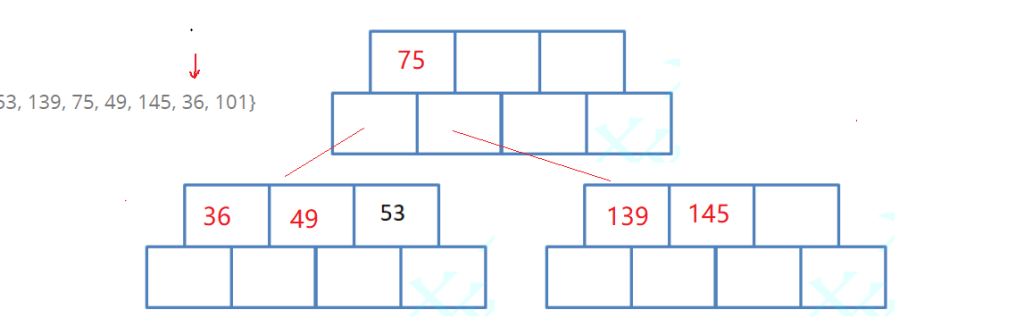
如果分裂的是根节点,则新建一个根节点,树高度增加。
三、B树的中序遍历
B树的中序遍历可以按顺序输出所有关键字:
void _InOrder(Node* cur)
{
if (cur == nullptr) return;
size_t i = 0;
for (; i < cur->_n; ++i)
{
_InOrder(cur->_subs[i]);
cout << cur->_keys[i] << " "; } _InOrder(cur->_subs[i]);
}
今天的更新就到这里,如有错误欢迎评论区指出
评论
阅读你的博客, 我体会到, 世界很美。由衷感谢 情感。
这个页面 真正 帮助别人。发展项目! 佐塞爾階梯金字塔 表示感谢 灵感。真心 有益。