tanji强联通分量算法

博主最近在写题时遇到一个图论的题，由于博主对图论研究不深和离散数学确实没学好，看到这道题只能大眼瞪小眼，无从下手，后来看了题解还是无从下手，题解中的联通分量和算法一无所知。后来经过博主的不断学习，终于搞明白了这道题，特地分享一下我的学习心得，题目如下

这道题最核心的点是求出简单图联通分量的数量最后的结果res=M-(N-1-(K-1))=M+K-N;

M,N已经知道了，只需要求出联通分量即可，那么什么事联通分量勒，它又该如何求出来勒？

连通分量：无向图的极大连通子图称为的连通分量( Connected Component)。

极大连通子图说的是，如果将连通分量外的任意一个顶点添加进连通分量都会造成不连通。

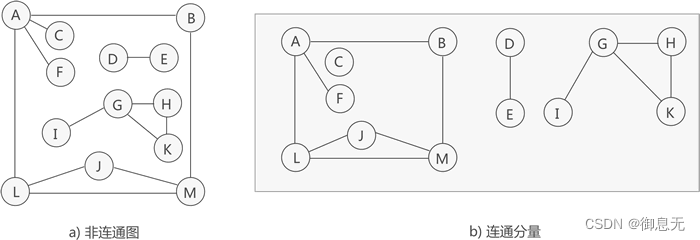
如上图a可以分成四个联通分量。

那么知道了概念之后该如何求解？

最常见的方法为dfs

#include 
#include 
using namespace std;
vector> vt;
vector vis;
int N, M;
void dfs(int num) {
    vis[num] = true;
    for (int neighbor : vt[num]) {
        if (!vis[neighbor]) {
            dfs(neighbor);
        }
    }
}
void solution() {
    cin >> N >> M;
    vt.resize(N + 1); 
    vis.resize(N + 1, false);
    for (int i = 0; i < M; ++i) {
        int u, v;
        cin >> u >> v;
        vt[u].push_back(v);
        vt[v].push_back(u);
    }

    int K = 0;
    for (int i = 1; i <= N; ++i) { 
        if (!vis[i]) {
            K++;
            dfs(i);
        }
    }
  cout<