二叉搜索树

二叉搜索树（Binary Rearch Tree）是二叉树的一种，他需要满足条件左子树的key大于右子树的key的条件.首先我们确定一个数组arr[6]={3,6,2,1,8,4},将其插入二叉搜索树中如图所示

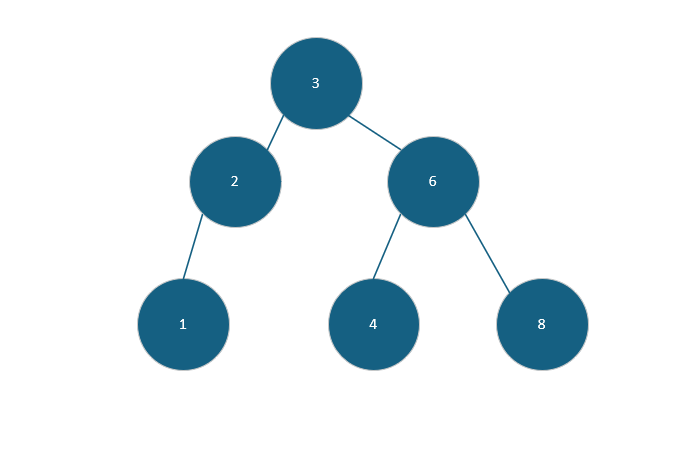
先插入3作为根节点，后面插入6,6>3作为3的子节点，后面插入2,2<3作为3的右子节点，依次类推，一颗二叉搜索树就完成了！

下面是代码实现：

C++:
template
struct BSTNode {
	K _key;
	BSTNode* _left;
	BSTNode* _right;
	BSTNode(const K& key) :_key(key)
		, _left(nullptr), _right(nullptr) {
	}
};
template
class BSTree {
	typedef BSTNode Node;
private:
	
	Node* _root = nullptr;
public:
	bool Insert(const K& key) {
		if (_root == nullptr) {
			_root = new Node(key);
			return true;
		}
		else {
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur != NULL) {
				if (cur->_key < key) {
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key) {
					parent = cur;
					cur = cur->_left;
				}
				else {
					cout << "错误，插入相等的值" << endl;
					return false;
				}
			}
			Node* newNode = new Node(key);
			if (parent->_key > key) {
				parent->_left = newNode;
			}
			else {
				parent->_right = newNode;
			}
			return true;
		}
	}
}

查找操作：

二叉搜索树的查找很简单，首先是根据key的值比较大小，要是大就往右查找，要是小就往左查找，要是循环到最后还是为空就没有找到返回为空实现代码如下所示：

c++:
bool Find(const K& key) {
	Node* cur = _root;
	while (cur) {
		if (cur->_key < key) {
			cur = cur->_right;
		}
		else if (cur->_key > key) {
			cur = cur->_left;
		}
		else {
			return true;
		}
		return false;
	}
}

删除操作：

搜索二叉树的删除操作是最难的，它分为四种情况

1.删除的节点的左右子树都为空：此时此节点为叶子节点，直接删除即可

2.删除的节点左为空：此时将删除节点的父节点指向删除节点的右子树

3.删除的节点右为空:此时将删除节点的父节点指向删除节点的左子树

4.删除节点左右子树都不为空：此时这种情况我们需要使用替代法，首先去即找到该节点的右子树的最小值/左子树的最大值，两个节点的值相互交换，再去删除节点。

下面是图演示：

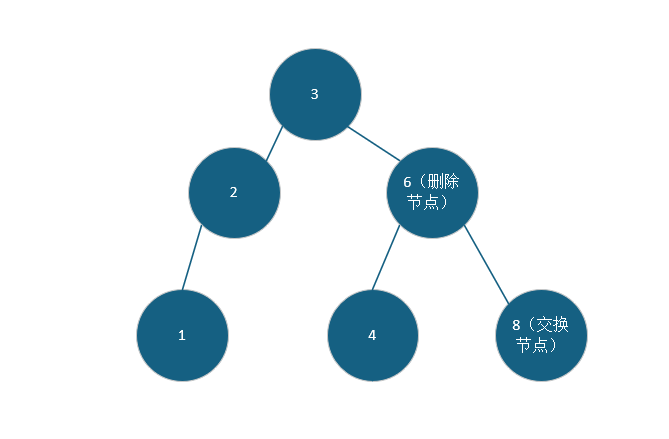
当删除6时，两边都有节点，我们就必须将8和6交换才能实现节点的删除。

下面是实习代码：

bool ERase(const K& key) {
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur != NULL) {
		if (cur->_key < key) {
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_key > key) {
			parent = cur;
			cur = cur->_left;
		}
		else {
			//删除
			//左为空
			if (cur->_left == nullptr) {
				if (cur == _root) {
					_root = cur->_right;
				}
				else {
					if (parent->_left == cur) {
						parent->_left = cur->_right;
					}
					else {
						parent->_right = cur->_right;
					}
				}
				delete cur;
			}
			else if (cur->_right == nullptr) {//右为空
				if (cur == _root) {
					_root = cur->_left;
				}
				else {
					if (parent->_right == cur) {
						parent->_right = cur->_left;
					}
					else {
						parent->_left = cur->_left;
					}
				}
				delete cur;
			}
			else {				//都不为空
				Node* replaceparent = cur;
				Node* replace = cur->_right;    //替代节点 
				while (replace->_left) {
					replaceparent = replace;
					replace = replace->_left;
				}
				cur->_key = replace->_key;
				if (replaceparent->_left == replace) {
					replaceparent->_left = replace->_left;
				}
				else {
					replaceparent->_right = replace->_right;
				}
				delete replace;
			}
			return true;
		}

	}
	return false;
}

值得注意的是：当删除节点为根节点时，我们需要额外提出来：如

if (cur == _root) {
_root = cur->_right;
}

而且当两边都有节点时我们也需要分情况：如果替代节点是其父节点的左子节点，更新父节点的左指针；否则更新父节点的右指针。

便利操作：

二叉树的节点遍历很简单，主要是通过递归遍历，博主这里就不一一列举，就以中序遍历为例子：

代码如下：

C++:

	void Inorder(Node* root) {
		if (root == nullptr) {
			return;
		}
		else {
			Inorder(root->_left);
			cout << root->_key << " ";
			Inorder(root->_right);
		}
	}
};

今天的博客就写到这里，如有问题请在帖子下面留言谢谢！！！