红黑树的实现

红黑树是搜索二叉树的一种，与平衡二叉树相近，搜索的时间复杂度可为logn,效率很高，与红黑树不同的是他颜色（红 黑）的规则，通过这个规则去控制二叉树的 高度。

红黑树的规则： 1.每个节点不是红色就是黑色
2.根节点是黑色
3.任意一条路径不会有连续的红色节点
4.每条路径都有相同的黑色节点数量
5.空节点都为黑色
红黑树节点的颜色枚举

下面是一棵符合规则的红黑树

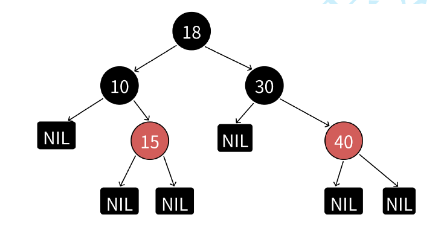
他的根节点为空，注意空节点也算一个黑色节点

下面是红黑树的代码实现

首先是节点的定义，与前面的平衡二叉树（见博主前面的文章介绍）相同

enum Colour
{
RED,
BLACK
};

template
struct RBTreeNode
{
// 这里更新控制平衡也要加入parent指针
pair _kv;
RBTreeNode* _left;
RBTreeNode* _right;
RBTreeNode* _parent;
Colour _col;

RBTreeNode(const pair& kv)
    :_kv(kv)
    , _left(nullptr)
    , _right(nullptr)
    , _parent(nullptr)
{
}

}; 此处唯一不同的就是定义了一个color去定义红黑树颜色

下面是插入操作，插入操作是二叉搜索树，平衡二叉树，红黑树最大的不同，二叉搜素树无需去控制树的高度，平衡二叉树则通过平衡因子控制树的高度，而我们的红黑树则通过上面四条规则控制二叉树的高度，他分几种情况 case1:当插入的父节点为黑色时直接插入返回 case2:当插入节点的uncle节点存在且为空（如图）g节点为granderfater节点，u节点为uncle节点，c节点为current节点，p节点为parent节点。当他存在且为红色时只需要循环变色即可，将p节点置为红色，p,u节点置为黑色，一直循环到p节点为空

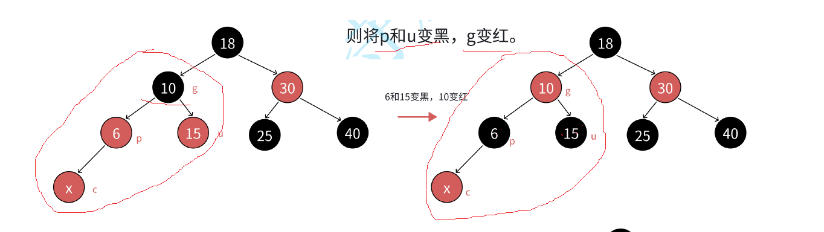
case3:当u结点为空时或者u节点为黑色，就需要利用上一篇文章的方法进行旋转，如下图：

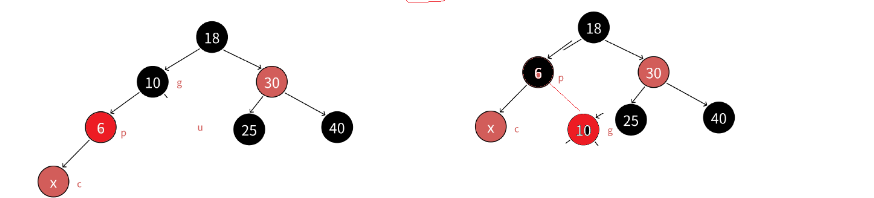
将g节点进行右旋再将颜色变化

case4：case3的情况并且插入在p节点的右边如图：

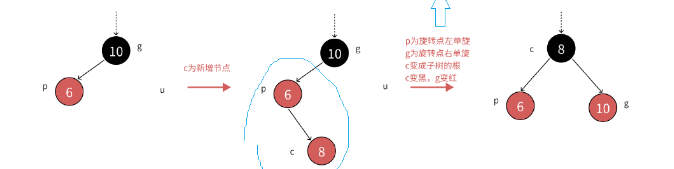
这时候就需要去双旋先对p节点进行旋转，后对g节点进行旋转

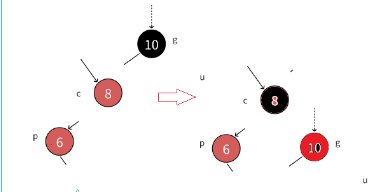
这是中间过程

下面是实现代码：、

bool Insert(const pair& kv)
{
	if (_root == nullptr)
	{
		_root = new Node(kv);
		_root->_col = BLACK;

		return true;
	}

	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (cur->_kv.first < kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_kv.first > kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}

	cur = new Node(kv);
	cur->_col = RED;
	if (parent->_kv.first < kv.first)
	{
		parent->_right = cur;
	}
	else
	{
		parent->_left = cur;
	}
	// 链接父亲
	cur->_parent = parent;

	// 父亲是红色，出现连续的红色节点，需要处理
	while (parent && parent->_col == RED)
	{
		Node* grandfather = parent->_parent;
		if (parent == grandfather->_left)
		{
			//   g
			// p   u
			Node* uncle = grandfather->_right;
			if (uncle && uncle->_col == RED)
			{
				// 变色
				parent->_col = uncle->_col = BLACK;
				grandfather->_col = RED;

				// 继续往上处理
				cur = grandfather;
				parent = cur->_parent;
			}
			else
			{
				if (cur == parent->_left)
				{
					//     g
					//   p    u
					// c
					RotateR(grandfather);
					parent->_col = BLACK;
					grandfather->_col = RED;
				}
				else
				{
					//      g
					//   p    u
					//     c
					RotateL(parent);
					RotateR(grandfather);
					cur->_col = BLACK;
					grandfather->_col = RED;
				}

				break;
			}
		}
		else
		{
			//   g
			// u   p
			Node* uncle = grandfather->_left;
			// 叔叔存在且为红，-》变色即可
			if (uncle && uncle->_col == RED)
			{
				parent->_col = uncle->_col = BLACK;
				grandfather->_col = RED;

				// 继续往上处理
				cur = grandfather;
				parent = cur->_parent;
			}
			else // 叔叔不存在，或者存在且为黑
			{
				// 情况二：叔叔不存在或者存在且为黑
				// 旋转+变色
				//   g
				// u   p
				//       c
				if (cur == parent->_right)
				{
					RotateL(grandfather);
					parent->_col = BLACK;
					grandfather->_col = RED;
				}
				else
				{
					RotateR(parent);
					RotateL(grandfather);
					cur->_col = BLACK;
					grandfather->_col = RED;
				}

				break;
			}
		}
	}

	_root->_col = BLACK;

	return true;
}

其余代码与博主以前的文章AVL树的插入一样见http://120.76.99.214/index.php/2025/07/01/%e5%b9%b3%e8%a1%a1%e4%ba%8c%e5%8f%89%e6%90%9c%e7%b4%a2%e6%a0%91%ef%bc%88avl%ef%bc%89/

最后是测试代码：

define _CRT_SECURE_NO_WARNINGS 1

include

include"RBTree.h"

include"AVLTree.h"

include

include // for rand() and srand()

include // for time()

include // for high_resolution_clock

vector GenerateRandomData(int N) {
vector v;
v.reserve(N);
for (size_t i = 0; i < N; i++) { v.push_back(rand() + i); } return v; } using namespace std::chrono; void TestRBTree(const vector& data) {
RBTree t;
auto start = high_resolution_clock::now();
for (int e : data) {
t.Insert({ e, e });
}
auto stop = high_resolution_clock::now();
auto duration = duration_cast(stop - start);
cout << "RBTree 插入 " << data.size() << " 个元素的时间: " << duration.count() << " 毫秒" << endl;
}

void TestAVLTree(const vector& data) {
AVLTree t;
auto start = high_resolution_clock::now();
for (int e : data) {
t.Insert({ e, e });
}
auto stop = high_resolution_clock::now();
auto duration = duration_cast(stop - start);
cout << "AVLTree 插入 " << data.size() << " 个元素的时间: " << duration.count() << " 毫秒" << endl; } //// 插入一堆随机值，测试平衡，顺便测试一下高度和性能等 //void TestAVLTree2() //{ // size_t begin2 = clock(); // AVLTree t;
// for (auto e : v)
// {
// t.Insert(make_pair(e, e));
// }
// size_t end2 = clock();
//
// cout << "Insert:" << end2 - begin2 << endl; // cout << t.IsBalanceTree() << endl; // // cout << "Height:" << t.Height() << endl; // cout << "Size:" << t.Size() << endl; // // size_t begin1 = clock(); // // 确定在的值 // for (auto e : v) // { // t.Find(e); // } // // 随机值 // /for (size_t i = 0; i < N; i++) // { // t.Find((rand() + i)); // }/ // size_t end1 = clock(); // cout << "Find:" << end1 - begin1 << endl; //} int main() { // 初始化随机数种子 srand(static_cast(time(0)));

// 生成随机数据
const int N = 1000000; // 插入数量
vector data = GenerateRandomData(N);
TestAVLTree(data);
TestRBTree(data);
return 0;

}

红黑树和AVL树插入查找效率差不多

今天的更新就到这里了，如有不对之处，烦请指出，谢谢