用红黑树手撕map/set 及其迭代器的使用

c++ • 462 • 0

tgw 8 月前

本文代码已在gitee上开源代码仓库地址https://gitee.com/tgwTTT/c-lreant

学习之前建议先阅读博主以前的文章http://www.tgwttt.xyz/?p=124

本篇博客是对map/set的底层代码实现，map/set是c++中常用和重要的容器，二者底层实现逻辑一致，均为红黑树（如下图），仅仅是key/key-value的区别。

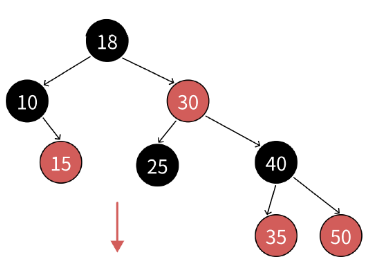
map和value的底层使用了相同的代码，虽然数据类型不一样，但是还是没有分开写，下面是代码的实现的分析。

首先为了区分pair,单独数据，他引入了仿函数去区分 map函数：

class map
{
struct MapKeyOfT
{
const K& operator()(const pair& kv)
{
return kv.first;
}
};

同理set函数的实现

class set
{
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
}; 将仿函数作为参数传入红黑树以达到函数数据的一致性故底层红黑树的定义为：

template
class RBTree
{
typedef RBTreeNode Node;

private:
Node* _root = nullptr; }

下面只需要修改一下插入函数pair Insert(const T& data)
{
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;

    //return pair(Iterator(_root, _root), true);
    return { Iterator(_root, _root), true };
}

KeyOfT kot;
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
    if (kot(cur->_data) < kot(data))
    {
        parent = cur;
        cur = cur->_right;
    }
    else if (kot(cur->_data) > kot(data))
    {
        parent = cur;
        cur = cur->_left;
    }
    else
    {
        return { Iterator(cur, _root), false };
    }
}

cur = new Node(data);
Node* newnode = cur;
cur->_col = RED;
if (kot(parent->_data) < kot(data))
{
    parent->_right = cur;
}
else
{
    parent->_left = cur;
}
// 链接父亲
cur->_parent = parent;

// 父亲是红色，出现连续的红色节点，需要处理
while (parent && parent->_col == RED)
{
    Node* grandfather = parent->_parent;
    if (parent == grandfather->_left)
    {
        //   g
        // p   u
        Node* uncle = grandfather->_right;
        if (uncle && uncle->_col == RED)
        {
            // 变色
            parent->_col = uncle->_col = BLACK;
            grandfather->_col = RED;

            // 继续往上处理
            cur = grandfather;
            parent = cur->_parent;
        }
        else
        {
            if (cur == parent->_left)
            {
                //     g
                //   p    u
                // c
                RotateR(grandfather);
                parent->_col = BLACK;
                grandfather->_col = RED;
            }
            else
            {
                //      g
                //   p    u
                //     c
                RotateL(parent);
                RotateR(grandfather);
                cur->_col = BLACK;
                grandfather->_col = RED;
            }

            break;
        }
    }
    else
    {
        //   g
        // u   p
        Node* uncle = grandfather->_left;
        // 叔叔存在且为红，-》变色即可
        if (uncle && uncle->_col == RED)
        {
            parent->_col = uncle->_col = BLACK;
            grandfather->_col = RED;

            // 继续往上处理
            cur = grandfather;
            parent = cur->_parent;
        }
        else // 叔叔不存在，或者存在且为黑
        {
            // 情况二：叔叔不存在或者存在且为黑
            // 旋转+变色
            //   g
            // u   p
            //       c
            if (cur == parent->_right)
            {
                RotateL(grandfather);
                parent->_col = BLACK;
                grandfather->_col = RED;
            }
            else
            {
                RotateR(parent);
                RotateL(grandfather);
                cur->_col = BLACK;
                grandfather->_col = RED;
            }

            break;
        }
    }
}

_root->_col = BLACK;

return { Iterator(newnode, _root), true };

}

void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;

parent->_left = subLR;
if (subLR)
    subLR->_parent = parent;

Node* pParent = parent->_parent;

subL->_right = parent;
parent->_parent = subL;

if (parent == _root)
{
    _root = subL;
    subL->_parent = nullptr;
}
else
{
    if (pParent->_left == parent)
    {
        pParent->_left = subL;
    }
    else
    {
        pParent->_right = subL;
    }

    subL->_parent = pParent;
}

}

void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;

Node* parentParent = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (parentParent == nullptr)
{
    _root = subR;
    subR->_parent = nullptr;
}
else
{
    if (parent == parentParent->_left)
    {
        parentParent->_left = subR;
    }
    else
    {
        parentParent->_right = subR;
    }
    subR->_parent = parentParent;
}

}

Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < key) { cur = cur->_right;
}
else if (cur->_kv.first > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}

return nullptr;

}

其余与上篇文章均相同，只需去替代key的值即可

下面是迭代器的实现，迭代器的实现很简单主要是*it++时的实现，看下图

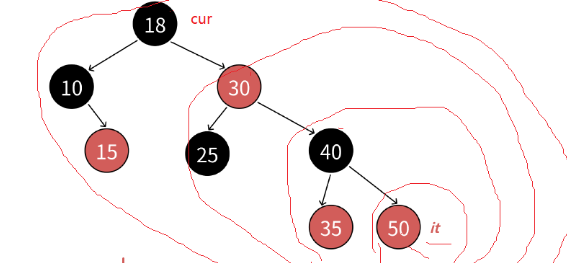
当it为空时结束循环我们查找时，遵循查找右子树最最左边的值，如查找10的下一位就是15 当右子树为空是，我们就循环找找到孩子是父亲左边的祖先，如查找15的下一位时就必须向上查找直到找到18

下面是代码实现

template
struct RBTreeIterator
{
typedef RBTreeNode Node;
typedef RBTreeIterator Self;

Node* _node;
Node* _root;


RBTreeIterator(Node* node, Node* root)
    :_node(node)
    , _root(root)
{
}

Self operator++()
{
    if (_node->_right)
    {
        // 右不为空，中序下一个访问的节点是右子树的最左(最小)节点
        Node* min = _node->_right;
        while (min->_left)
        {
            min = min->_left;
        }

        _node = min;
    }
    else
    {
        // 右为空，祖先里面孩子是父亲左的那个祖先
        Node* cur = _node;
        Node* parent = cur->_parent;
        while (parent && cur == parent->_right)
        {
            cur = parent;
            parent = cur->_parent;
        }

        _node = parent;
    }

    return *this;
}

Self operator--()
{
    if (_node == nullptr)  // --end()
    {
        // --end()，特殊处理，走到中序最后一个结点，整棵树的最右结点
        Node* rightMost = _root;
        while (rightMost && rightMost->_right)
        {
            rightMost = rightMost->_right;
        }
        _node = rightMost;
    }
    else if (_node->_left)
    {
        // 左子树不为空，中序左子树最后一个
        Node* rightMost = _node->_left;
        while (rightMost->_right)
        {
            rightMost = rightMost->_right;
        }
        _node = rightMost;
    }
    else
    {
        // 孩子是父亲右的那个祖先
        Node* cur = _node;
        Node* parent = cur->_parent;
        while (parent && cur == parent->_left)
        {
            cur = parent;
            parent = cur->_parent;
        }
        _node = parent;
    }

    return *this;
}

Ref operator*()
{
    return _node->_data;
}

Ptr operator->()
{
    return &_node->_data;
}

bool operator!= (const Self& s) const
{
    return _node != s._node;
}

bool operator== (const Self& s) const
{
    return _node == s._node;
}

};

今天的更新就到这里，如有不对，烦请留言，谢谢！！

6 赏

‹ 上一篇

下一篇 ›

作者尚未添加打赏二维码！

用红黑树手撕map/set 及其迭代器的使用

相关文章

评论

我是萌萌哒的侧边栏！