建议阅读本文前先阅读上篇文章http://www.tgwttt.xyz/?p=187
接上文,本文主要谈论堆排序和Top_k问题。
一.堆排序:
堆排序建堆共有两种方法:向上调整建堆和向下调整建堆。
现在我们分别来分析一下两者的优劣:
向上调整建堆:
void AdjustUp(HPDataType* a, int child)
{
// 初始条件
// 中间过程
// 结束条件
int parent = (child - 1) / 2;
//while (parent >= 0)
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
for (int i = 1; i < n; i++)
{
AdjustUp(a, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}向上调整建堆:是利用堆的插入,然后再向上调整。
下面是时间复杂度的计算:
T(n)=k=0∑h−22k⋅(h−1−k)
T(n)=20⋅(h−1)+21⋅(h−2)+22⋅(h−3)+⋯+2h−2⋅1
再使用错位相减法:
T(n)=[2(h−1)−(h−1)]+[4(h−2)−2(h−2)]+⋯+[2h−1⋅1−2h−2⋅1]−2h−1⋅0=
(h−1)+2(h−2)−2(h−2)+4(h−3)−4(h−3)+⋯+2h−2⋅1−2h−2⋅1+2h−1⋅1=
k=0∑h−22k−(h−1)⋅20+2h−1⋅1=(2h−1−1)−(h−1)+2h−1=
-N+(N+1)log(N+1)-1
时间复杂度为N*log(2)N
向下调整建堆:
void AdjustDown(HPDataType* a, int n, int parent)
{
// 先假设左孩子小
int child = parent * 2 + 1;
while (child < n) // child >= n说明孩子不存在,调整到叶子了
{
// 找出小的那个孩子
if (child + 1 < n && a[child + 1] < a[child])
{
++child;
}
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
与向上调整建堆相比:向下调整建堆则是从(n-2)/2,开始调整堆。
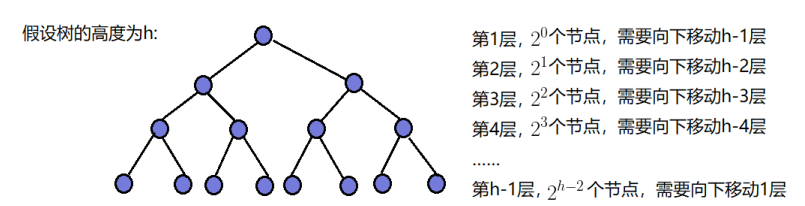
时间复杂度计算:
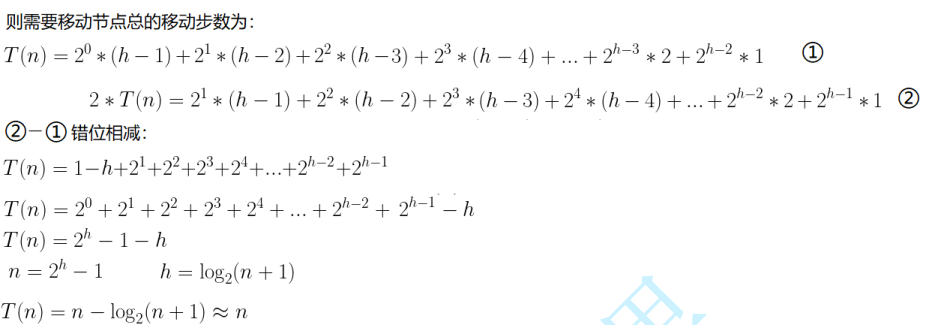
可知向上调整建堆劣于向下调整建堆
二.TOP_K问题
top_K问题是从N个数中快速找到前K个大的数(N>>k)
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,
基本思路如下:
1. 用数据集合中前K个元素来建堆前k个最大的元素,则建小堆前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
但是上述问题会出现一个问题:如果数据量太大。1e10呢?此时我们就需要4G,空间开销过大,如果只给你4M,你会怎么做呢?
答案是:先建一个K个数据大小的小堆,再让其他剩下的数与之堆顶比较,若大于栈顶的元素,则入堆,换掉栈顶的元素,向下调整。
今天的更新,就到这里如有错误欢迎指出!!!
评论
还没有任何评论,你来说两句吧!